I was recently introduced to the thoughts of the science philosopher and scientist Michael Polanyi by Dr. Helge Brovold. As I was reading Polanyi’s book “The tacit dimension” (1966), which I borrowed from Helge, I realized that Polanyi’s description of tacit knowledge had a statistical counterpart, which I write about here. As it turns out this statistical detour may teach us how tacit knowledge is  implemented in our brains. Read on if this sounds interesting!

The human brain is an incredible pattern recognizer. Just think about it; among the hundreds or thousands of faces you see every day, most of which just pass by unnoticed, you recognize a familiar face within a fraction of a second. But, do you really know how you know a face? Can you describe the face of an acquainted person without seeing him or her? Probably not, you just know them when you see them. Michael Polanyi refers to this ability as “tacit” knowledge. Sometimes you just know, without knowing how you know!

Polanyi uses the blind with his stick as an example. After long time exercise the stick starts to function as an extension of the hand of the blind, and he can almost “feel” the tip of the stick as he walks down the street. He does not know exactly how he can feel the tip so vividly, he just does. He has tacit “bodily” knowledge that he can’t express in words.

I have another example of more abstract tacit knowledge from my personal life. In addition to being a statistician, I am a hobby ornithologist. Since I was a small boy I have enjoyed bird watching, and after about 35 years of experience, I have acquired a certain level of tacit knowledge with regard to bird identification. Sometimes, just a short glance is enough to identify the bird, but if you ask me how I recognized it, I may be unable to point to the specific feature that “gave it off”. Among bird watchers this is well known, and they often refer to this as “jizz”.

Polanyi describes the tacit dimension as a relation between something which is close to us (he calls it the proximal part) and something which is farther from us (the distal part). We use the proximal part as an extension of ourselves to understand or predict the distal part.

By integrating and internalizing the proximal part, we become able to use it as a tool for pointing our attention towards the distal part.

However, the rules, or the model if you like, which is formed by the integration of the proximal part may be unknown to us! The mind uses the observable distal part as a supervisor in the integration process to form an unconscious model for attention.

So, where is the statistical connection in this story?

The aim of statistical inference is often to build a model to connect a set of easily observable input variables (X) to one (or several) desired output variable(s) (Y). The purpose is typically to use the estimated model for prediction. Just think of the weather forecast as an example. Given today’s air pressure, temperature and wind (X), what is tomorrow’s weather (Y) going to be?  Once found, the estimated model may be used to map newly observed inputs into predicted outputs. The output variable, often referred to as the response, is the quantity at which we point our attention. We may therefore consider the response variable as the distal part in Polanyi’s tacit relation. The input variables (X) is the proximal part.

My interpretation of Polanyi is that the distal part (be it a problem to be solved, a meaning to be understood, or a context to be explored) serves as the target guiding the integration process of the proximal part. Exactly how the integration is done is not important, and the final “model” may lies as a tacit construct in our sub-consciousness. The important thing is that the model serves as a good predictor for the target!

Now, this equals what we statisticians call supervised statistical learning. It is supervised because the target is known, at least in the process of learning. The integration process of Polanyi parallels the estimation of some model f(X) which connects the distal part to the proximal part, like

Y = f(X) + e

(The term e is the noise term summing up the variation in the response, which can’t be explained by the model.)

Some may now object by saying that the integrated proximal part in statistical learning, the estimated model, is not tacit because the model is chosen subjectively by the statistician. The statistician thus has detailed information about the model, and perfectly knows how the input is connected to the response. This does not sound very tacit!

No, but there is a special class of algorithmic statistical models in supervised learning which does fit into the tacit dimension, and, in fact, the models are inspired by our brain network. They are known as artificial neural networks (ANN).

 

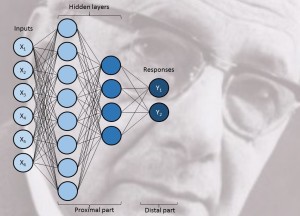
The model f(X) of an ANN is not completely defined by the data analyst. As shown in the Figure, the algorithm assumes one or multiple layers of “neurons” connecting the input variables X with the response Y. One or several hidden layers of neurons are connected to X and Y and each connection is a linear or non-linear mapping of information with parameters trained from data in such a way that the distal part Y is approximated as close as possible. The first hidden layer may for instance summarize simple patterns observed in X, which are further categorized in the second layer, and so on. In this way an AAN may be used to model highly non-linear and complex output features.

The training of the neural connections is to a large extent left to the computer, and the resulting models may be quite complex, and the ANN models have been criticized for being too much of a black box and difficult to understand… Exactly! What goes on in the model is hidden, it is tacit!

The tacit dimension of our brain is probably quite similar. After all, the artificial neural networks are inspired by the biological neural networks… The neural networks may be trained to connect a set of perceived inputs to a target output in a way which is hidden to us and buried in our unconsciousness.  Beneath our consciousness our brains perform multivariate, statistical AND tacit modeling, and recent research has indicated that the cerebellum may play a key role in unconscious integration of inputs and facts, like I wrote about in a previous post “Google pedagogics”.

The artificial neural networks are as mentioned highly flexible, and there is always a risk of over-fitting the model, that is, the model fits the observed outputs of the training data too well, and the model is likely trying to explain noise in the response. This reduces the predictive performance of the model for new observations, and in order to reduce this problem it is customary to “prune” the networks by removing some “weak” connections in order to make is less complex and less vulnerable to random fluctuations in the response. As I wrote in my previous post new theories about the effect of sleeping suggest that there is natural pruning going on in our brain during the NREM phase of our sleep. Hence, it appears that our brain is also fine-tuning our tacit knowledge during sleep, making it for efficient for later use.

So, to sum it all up, our brain appears to have the ability to use its biological neural network to integrate proximal information into a flexible model which can be used to understand or predict a distal target or response, and sometimes this is a completely unconscious and tacit process.

All our brain lets us know… is that we know…!

Reference:

Polanyi, M. (1966). The tacit dimension. Doubleday, N.Y. US.